数字的二进制表示
●数字的二进制表示数字13.125示例如下图,规则如下:
(1)整数部分不断除以2记录余数直到商为0,将余数逆序排列作为结果;
(2)小数部分不断乘以2记录去掉整数部分直到乘积小数部分结果为0,将整数部分正序排列作为结果;

IEEE-754的64位浮点数
●JavaScript默认采用IEEE-754的64位浮点格式存储数字;
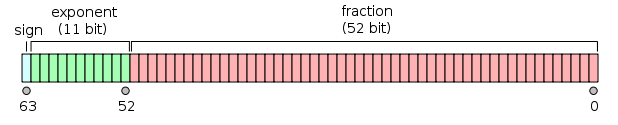
●IEEE-754的64位浮点数存储方式使用64位存储浮点数,并将64位划分为1位符号位、11位指数位、52位尾数位三部分,具体如下。
(1)符号位(sign):0表示正数,1表示负数,这也是为什么会出现+0和-0的原因;
(2)指数位(exponent):表示次方数,由于指数分正负,约定中间数(二进制011 1111 1111,即2^10-1=1023)对应的真值是0,于是“真值=存储值-1023”(所以最高位是1时是正数,最高位是0时是负数或零),约定存储值的最小值000 0000 0000(真值-1023)与最大值111 1111 1111(真值1024)作特殊用途,所以指数位真值取值的范围是[-1022, 1023],这个范围内的数字称为normal number;
(3)尾数位(fraction):表示尾数,尾数位超出部分采用进1舍0;
●数字存储前先将其转为二进制下的科学计数法的形式,为了最大限度使用存储空间,存储normal number时将科学计数法中“1.”前缀省略,从而可以让精度多一位变成53位,按照“(−1)^sign×(1.fraction)×2^(exponent−1023)”计算真值;
●存储绝对值小于normal number范围的数字(称为subnormal number)时,不再限制先转换为1.0前缀的科学计数法从而可表示更小的数字(小至2^(-(1022+52))=2^(-1074)),存储submormal number的标识是指数位存储值为全0,此时按照"(−1)^sign×0.fraction×2^(−1022)"计算真值(指数位取值-1022而不是按照"exponent-1023"计算,因为subnormal number相比normal number不省略"1.0"前缀相当于小数点多左移了一位,即0.10×2^(-1022)===1.0×2^(-1023));
●指数位存储值为全1对应的特殊值:
(1)尾数位为全0时,表示值为Infinity;
(2)尾数位非0时,表示NaN,尾数位存储空间被称为NaN的payload,可用于存储相关信息比如何原因导致的NaN;
●数字13.125按照IEEE-754标准存储到64位空间的过程:
(1)数字转为二进制形式,即1101.001;
(2)转为二进制下的科学计数法,即1.101001×2^3,存储0.101001小数点后部分到尾数位,指数位存储3+1023=1026转二进制=10000000010;
(3)于是64位空间所存储内容为0 10000000010 1010010000000000000000000000000000000000000000000000
●双精度下的安全整数范围是[-2^53, 2^53],因为只能存储53位有效数字位,超过53位的有效数字位将丢失,超出安全整数范围的值只要有效数字位不超过53位还是可以正确存储的,如2^54、2^100;
IEEE-754的32位浮点数
●IEEE-754存储浮点数都是将存储空间划分为符号位、指数位、尾数位,以下是单精度32位浮点数各区域的划分位数,存储方式与64位同理;
